概述:
测量要素在几何平均中心周围的集中或分散程度。

Mitchell, Andy. The ESRI Guide to GIS Analysis,Volume 2. ESRI Press, 2005.
**
公式:
**
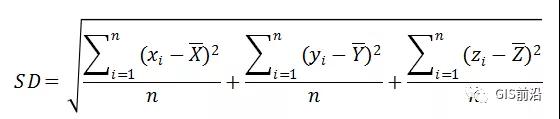
其中 xi ,yi和zi为要素 i 的坐标,{x̄, ȳ, z̄} 表示要素的平均中心,n 为要素总数。
加权标准距离扩展如下:
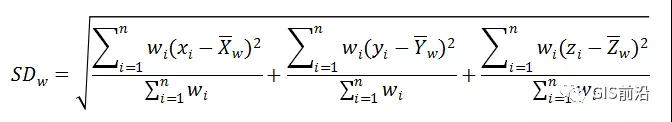
其中 wi 是要素 i 的权重,{xw, yw, zw} 表示加权的平均中心。
说明:
1、输出:
标准距离工具可创建一个新要素类,其中包含以平均中心点为中心的圆面(如果指定了案例分组字段,则每个案例分别对应一个中心和一个圆)。绘制每个圆面时使用的半径均等于标准距离值。各圆面的属性值包括圆平均中心 x 坐标、平均中心 y 坐标和标准距离(圆半径)。
2、注意事项:
此工具需要使用投影数据来准确测量距离。
如果要素的基础空间模式是朝向中心处集中而朝向外围的要素较少(符合瑞利分布),则一个标准差圆大小会包含聚类中约 63% 的要素,两个标准差圆大小会包含聚类中约 98% 的要素,三个标准差圆大小则可包含两个维度中约 99% 的要素。
可以根据可选的权重字段参数计算标准距离(例如,获得按工作人员衡量的企业标准距离)。权重字段应为数值型字段。
案例分组字段参数用于在分析前对要素进行分组。当指定了案例分组字段时,会首先根据案例分组字段值对输入要素进行分组。然后计算每个组的标准距离圆。案例分组字段可以为整型、日期型或字符串型,并以属性形式显示在输出标准距离要素类中。对于案例分组字段,具有空值的记录将从分析中排除。
试验:
我们以粤港澳大湾区为例,以密密麻麻的交通信号灯点数据为分析数据,数据源来自OSM:

在Spatial Statistics Tools中的度量地理分布-标准距离可以找到:
上述已经讲到,一个标准差圆大小会包含聚类中约 63% 的要素,两个标准差圆大小会包含聚类中约 98% 的要素,三个标准差圆大小则可包含两个维度中约 99% 的要素。
我们先采用默认的一个标准距离观察结果:
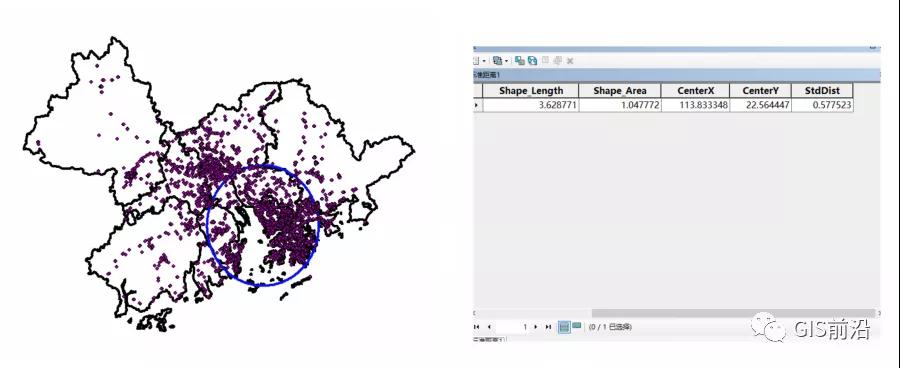
会发现生成了一个圆,这个圆的属性表中给出了圆心的X/Y坐标以及标准距离,即圆的半径,那么我们就可以根据这个结果进行描述:“在XXX°E,XXX°N,以XXX米为半径扩展出去的圆可以囊括大湾区约68%的交通灯…”
当然,细心的可以观察到,标准距离其实并不是以米为单位的,这是我们需要对源数据进行投影,不然的话我们得到的都是以度为单位的,我们投影过后生成的圆与属性表如下:
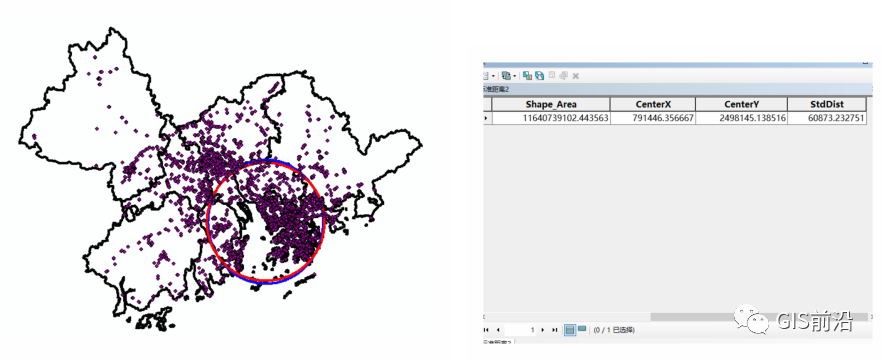
此时的XY坐标都变成了平面坐标,标准距离变成了米为单位的长度,那么很明显,就是60.8公里范围。
当然,源数据中有许多的类别,比如说高速路口处的等、人行道的灯、普通信号灯等等,大家可以类似将之想象成不同类别的研究对象,比如说我想统计某个区域内的所有不同类别的动物,但是我只有一个点图层,这个点图层里包括了大象、老虎、斑马等等,那我们在案例分组字段中选择该类别就可以了:
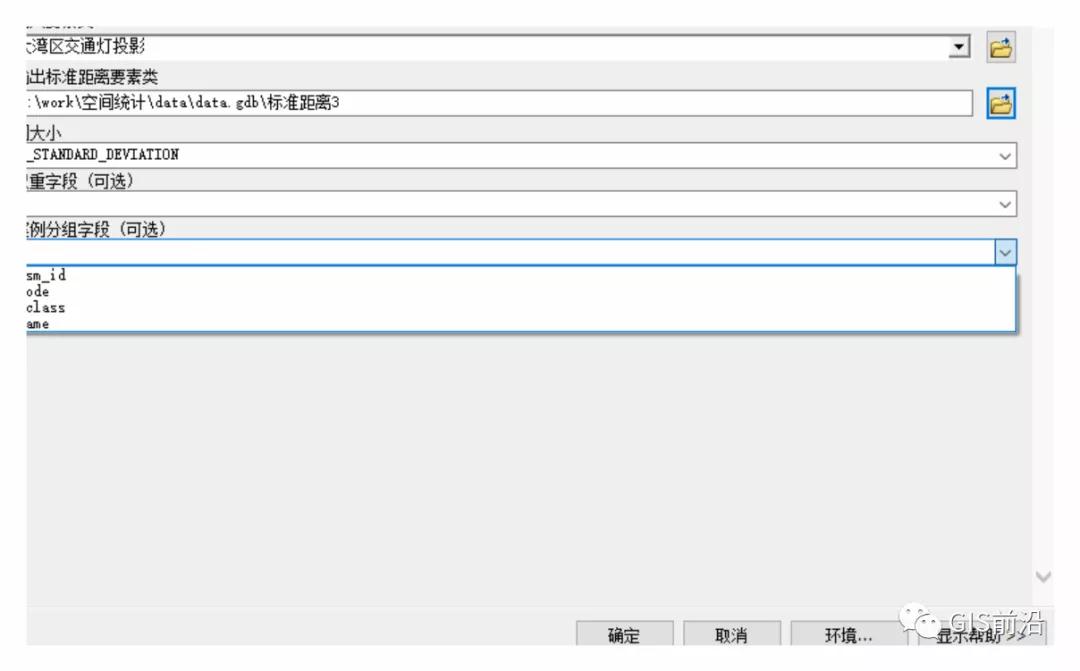
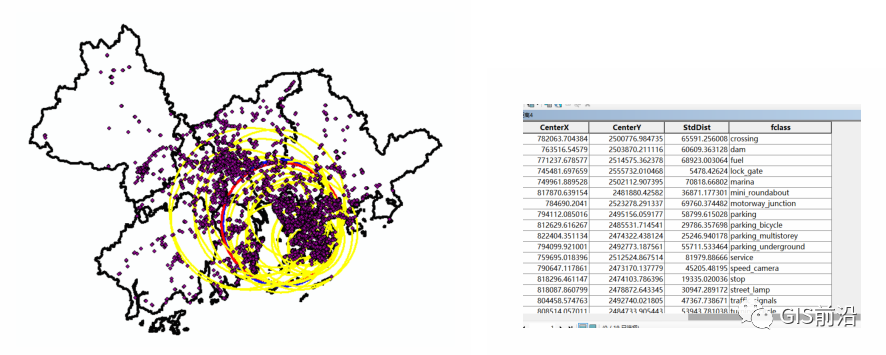
这样他会根据每一类别生成标准距离圆以及他们的中心坐标、标准距离:
最后,我们如果选择两个标准距离,那么也就如同之前讲的一样,它会囊括我们数据的98%,但是无论是1、2、3个平均距离,他们的中心点都是一样的:
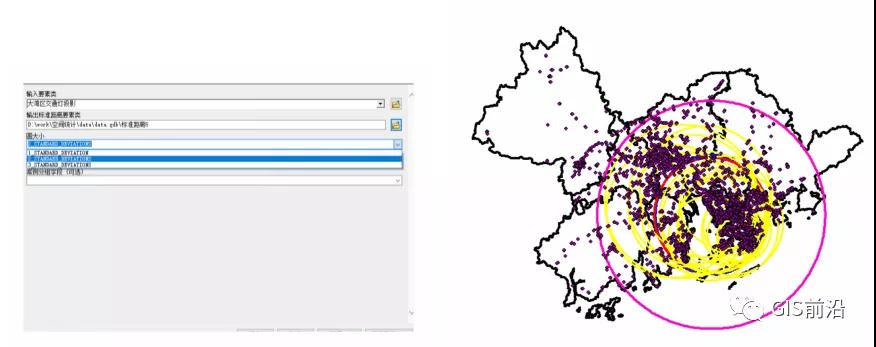
那么此时,我们就可以根据这个结果进行描述:“在XXX°E,XXX°N,以XXX米为半径扩展出去的圆可以囊括大湾区约98%的交通灯…”
根据ArcGIS中的简单的标准距离工具,我们就可以对我们收集到的空间数据进行详细的描述,并且可以直接根据结果进行出图,这实在是太方便了!













